Bem-vindos!!!!

Nesta página o professor Rodrigo Melo de Matemática orientará seus alunos.

Bons estudos.

Matemática - Rodrigo Melo - 1D 

Orientação: A atividade deve ser confeccionada em folha de caderno à parte e posteriormente entregue ao professor quando ocorrer o retorno das aulas presenciais.

Atividade 1:

Pesquise e elabore um resumo sobre os seguintes tópicos:

• Regularidade numérica e geométrica
• Sequências
• Progressão Aritmética
• Progressão Geométrica:

Atividade 2:

O QUE É A SEQUÊNCIA DE FIBONACCI?

Ela está presente em muitas coisas do nosso cotidiano: nas mãos, no rosto, nos cartões de crédito e até nas pirâmides do Egito!

É uma sucessão de números que, misteriosamente, aparece em muitos fenômenos da natureza.

Descrita no final do século XII pelo italiano Leonardo Fibonacci, ela é infinita e começa com 0 e 1. Os números seguintes são sempre a soma dos dois números anteriores. Portanto, depois de 0 e 1, vêm 1, 2, 3, 5, 8, 13, 21, 34...

Ao transformar esses números em quadrados e dispô-los de maneira geométrica, é possível traçar uma espiral perfeita, que também aparece em diversos organismos vivos. Outra curiosidade é que os termos da sequência também estabelecem a chamada “proporção áurea”, muito usada na arte, na arquitetura e no design por ser considerada agradável aos olhos. Seu valor é de aproximadamente 1,618 e, quanto mais você avança na sequência de Fibonacci, mais a divisão entre um termo e seu antecessor se aproxima desse número. [...]

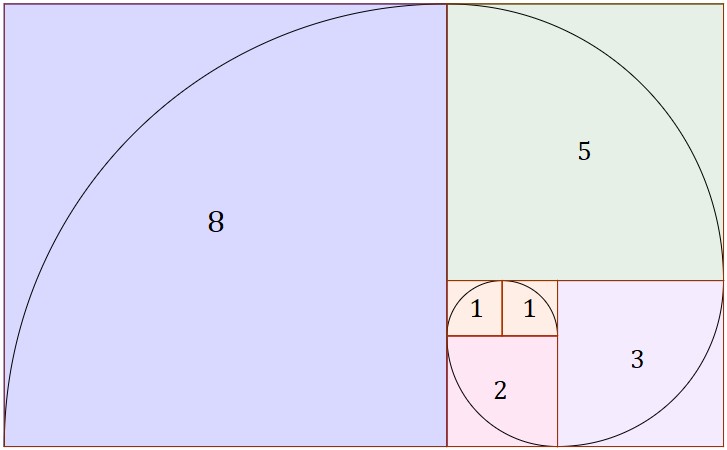
Segundo o texto, a sequência ou espiral de Fibonacci é infinita e começa com 0 e 1. Os números seguintes são sempre a soma dos dois números anteriores. Portanto, depois de 0 e 1, vêm 1, 2, 3, 5, 8, 13, 21, 34, … e, seguindo o padrão, podemos estabelecer que o 0 ocupa a posição zero, o número 1 a primeira e a segunda posição, o 2 fica na terceira posição, o número 3, a quarta, e assim sucessivamente. Com base nessas informações:

1. Qual é o número que se localiza na 10a posição?
2. Quais são os números que ocupam as cinco próximas posições, posteriores à 10a (11a, 12a etc.)?
3. Utilizando n para determinar a posição e f(n ) como o número que corresponde a eu posicionamento, temos:

f(0) = 0 f(1) = 1 f(2) = 1 f(3) = 2 f(4) = 3

d. Determine uma lei de formação de f(n ) para n > 2.Onde mais você imagina que haja sequências como as vistas até aqui? Faça uma pesquisa para verificar e traga os resultados para compartilhar com seus colegas.

 Atividade 3:

Observe a sequência:                                 

1. Escreva o padrão observado na sequência acima.
2. Qual é o 8º elemento da sequência?
3. Qual é o 14º elemento da sequência?
4. Tente responder, sem desenhar, qual é o elemento que ocupa a 20ª posição? Escreva como chegou a essa conclusão.
5. Qual será a ordem dessas figuras nas posições 179, 180 e 181? Escreva como chegou a essa conclusão.

Atividade 4:

Analise a sequência abaixo:

1. Como você vê o crescimento do padrão nessa sequência? Escreva com suas palavras.
2. Quantos quadrados terá a figura 5 desta sequência?
3. Quantos quadrados terá a figura 6 desta sequência?
4. Quantos quadrados terá a figura 12 desta sequência?
5. Você poderia usar 190 quadrados para fazer uma estrutura tipo escada? Justifique matematicamente a sua resposta.
6. Complete a tabela abaixo e tente encontrar uma expressão que represente o número de quadrados na Figura n

 Atividade 5:

Você conhece o jogo Torre de Hanoi? Em caso negativo, conheça seu objetivo e suas regras na imagem abaixo.

1. : Se puder, aproveite para jogá-lo online em http://www.somatematica.com.br/jogos/hanoi/ e, para saber mais sobre esse jogo, acesse http://clubes.obmep.org.br/blog/torre-de-hanoi/ .

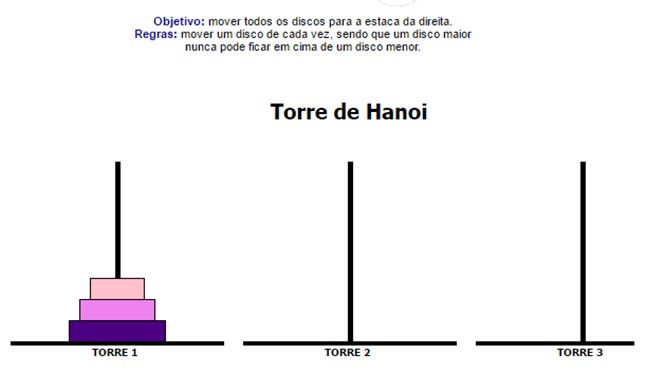
1. Na tabela abaixo, registre o número mínimo de movimentos necessários para atingir o objetivo proposto para cada número de discos indicado na tabela.

1. Qual é o número mínimo de movimentos necessários para mover 20 discos?
2. A última coluna da tabela acima (n) deve conter uma maneira de determinar o número mínimo de movimentos para qualquer que seja a quantidade de discos. Registre a forma como você chegou nessa representação.

 Atividade 6:

Escreva os cinco primeiro termos da sequência dos números ímpares positivos. Em seguida, responda:

1.  Qual é o 10° termo?
2. Qual é o termo a₁₃
3. Qual é o termo a₂₅
4. Como se pode determinar um termo a_n qualquer?

 Atividade 7:

Determine os cinco primeiros termos da sequência cujo termo geral é:

1. a_n = n² + 1
2. a_n = 3n – 2

Atividade 8:

Calcule a soma dos 20 primeiros termos da PA (2, 6, 10,....) 

Matemática - Professor Rodrigo Melo - 3TA - 3TB

 Orientação: A atividade deve ser confeccionada em folha de caderno à parte e posteriormente entregue ao professor quando ocorrer o retorno das aulas presenciais.

 Atividade 1:

Em nosso dia-a-dia, é muito comum necessitarmos comparar grandezas, como os preços no supermercado, os ingredientes de uma receita, a velocidade média e o tempo. E, quando comparamos, percebemos que existem situações em que, sabendo como uma das grandezas varia, podemos prever a variação da outra com o uso de cálculos matemáticos simples. Informalmente você já conhece e utiliza esses cálculos. Pretendemos aqui aprimorar esses conhecimentos para que você possa aplicá-los com mais confiança e consistência.

Leia, analise cada situação e responda às perguntas abaixo

Atividade 2:

Pesquise e elabore um resumo sobre os seguintes tópicos:

• Razão
• Proporcionalidade
• Regra de três simples e composta

Em seguida, faça um texto comparando o resultado de sua pesquisa com suas respostas na Atividade 1.

Atividade 3:

Tomando como base a pizza grande dividida em 8 pedaços, e considerando que cada pessoa coma 2 pedaços de pizza, qual o número máximo de pessoas que poderá participar de uma festa beneficente onde 150 pizzas serão servidas?

a) 800.      b) 600.     c) 400.      d) 100.

Atividade 4:

Uma avenida com 600m de comprimento está sendo asfaltada. Em 3 dias foram asfaltados 150 m da avenida. Supondo que o ritmo de trabalho continue o mesmo, em quantos dias os 600 m da avenida estarão asfaltados?

a) 9.      b) 12.      c) 15.        d) 18.

Atividade 5:

Em todo mapa deve existir proporcionalidade direta entre as grandezas: distância no desenho e distância real. A razão constante entre a distância no desenho e a distância real entre duas cidades é chamada de escala.

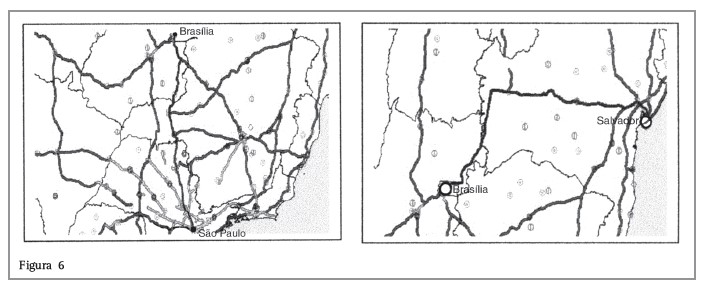
A escala utilizada neste mapa é:  , ou seja, a cada 1 cm no desenho correspondem 5.000.000cm = 50km no real.

Usando esse mesmo mapa, assinale V (verdadeiro) ou F (falso) para as afirmações a seguir:

a) Quanto maior for a medida, em cm, no mapa, menor será a distância entre as cidades. ( )

b) A uma medida de 30cm no mapa corresponde uma distância real de 2.000km. ( )

c) A distância Brasília-Salvador, que é de aproximadamente 1.400km, corresponde a 28 cm no mapa. ( )

d) Cada 3 cm no desenho corresponde a uma distância real de 15km. ( )

e) A distância São Paulo-Brasília, que é de aproximadamente 1.000km, está representada por 20cm. ( )

Atividade 6:

Nas situações abaixo, identifique as grandezas envolvidas, analise-as e verifique se elas variam numa proporcionalidade direta (PD) ou inversa (PI), ou se não existe necessariamente proporcionalidade (NP).

a) ( ) A medida do lado de um terreno quadrado e o perímetro desse terreno.

b) ( ) O ordenado de um carteiro e o número de cartas que ele distribui.

c) ( ) A distância percorrida por um automóvel e a quantidade de combustível consumida.

d) ( ) O número de pedreiros e o tempo gasto para construir um muro.

e) ( ) A idade de um jovem e seu peso.

f) ( ) A medida do lado de um terreno quadrado e a área desse terreno.

g) ( ) A quantidade de pó de café e o número de cafezinhos.

h) ( ) O número de acertadores da megassena e o valor do prêmio distribuído.

Atividade 7:

Para transportar areia para uma construção, foram usados 4 caminhões com capacidade de 3 m3 cada um. Para fazer o mesmo serviço e com base nessas informações, podemos concluir que:

a) se a capacidade de cada caminhão fosse de 6 m3, seriam necessários 8 caminhões.

b) quanto maior a capacidade do caminhão, menor será o número de caminhões necessários.

c) seriam necessários 10 caminhões, se a capacidade de cada caminhão fosse de 1m3.

d) a quantidade de caminhões não depende da capacidade de cada caminhão.

Atividade 8:

Faça os cálculos e responda:

Para os 180 clientes que responderam a pesquisa:

1. Quantos clientes representam 12% do total de clientes?
2. Quanto por cento do total de clientes representam 135 clientes?

Atividade 9:

Um litro de leite custava R$ 0,80 e sofreu um acréscimo de 15%. Qual será o novo valor do litro desse leite?

Atividade 10:

Solaine abriu com R$ 500,00 uma caderneta de poupança no dia 2 de maio. Não fez nenhum outro depósito durante o mês. Se o rendimento nesse mês foi de 0,7%, qual será o saldo de Solaine no dia 3 de junho?

a) R$ 503,50.      b) R$ 507,70.      c) R$ 535,00.            d) R$ 570,00.

POSTADO EM 04/05/2020